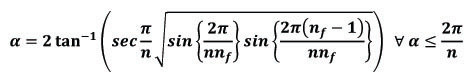About

Mathematician: HCR1991
Mr Harish Chandra Rajpoot, DOB: 20 January 1991, India

In the ancient world when the mathematics was not much advanced, it was not too difficult to develop concepts and derive theorems, & formulas but due to advancement in mathematical researches it is rather difficult but not impossible to invent new concepts, formulas or theories in the field of Mathematics in the present scenario. Although, it was his dream to find out some extra-ordinary things in the field of Mathematics as it was his interesting subject. He was much interested in Algebra, Geometry, Trigonometry, Calculus & Theoretical Physics since his early education especially Intermediate. He was not perfectly sure what was to discover, existing or non existing even in 21th century, but he made his mind to invent some extra-ordinary formula in Mathematics which had never been thought by any mathematician till his completing intermediate in 2009-2010. Really, he was much interested in deriving new concepts & formula rather to solve the existing problems of Mathematics & Physics, although he wasn't sure about anything but insisting to discover extra-ordinary, fond of dealing with the concepts, derivations & complex formula, causing him to go through the fundamentals with his own efforts, especially in Mathematics. However he is highly enthusiastic & valiant for new findings in Mathematics & never cares about it leading to any failure. He always likes to think freely about creating new concepts & formula. He is open-minded, free-minded & so daring that no failure can depress/frustrate him even a bit. However, in case of any failure, he simply changes his way of thinking & way of working.    

 

Mr Rajpoot belongs to a middle class family living in a rural village Buraura which is in the district Mahoba of state Uttar Pradesh in India. After passing his 8th class exam from Sardar Patel Junior High School, Kilhauwa (nearer to his village in Mahoba district) in 2005, he got admission to D.A.V. govt. Inter College (UP, Board) in district Mahoba (a historical place of ancient warriors) in 2006.

Unfortunately, he became seriously sick few weeks before to his exam & had to drop in 11th class in 2007 . After getting recovered, his father took him to Kanpur where he got admission to Oxford Model Inter Collage, (Hindi Medium, UP Board) Kanpur in 2008. He learnt a lot of things from his well experienced teachers & got in better environment with CBSE students in college hostel. It helped him very much to interact & communicate the CBSE students in English language. Thus with his own efforts he, being a Hindi Medium student, learnt many a concept of Mathematics & Physics from the books of English Medium students. He became the favorite student to his teacher of Physics Mr Upendra Sir who mentored & helped him a lot in his studies at the college as well as at his home & encouraged him for doing the best. He was appreciated for his better performance in Physics & Mathematics by his teachers, principal & manager of the college. Therefore, being inspired & encouraged, he developed a great interest & decided to make research in the field of Mathematics & Physics by his own efforts. Although, he was less interested in games & sports but he used to utilize most of his free time in Mathematical derivations, estimations/analysis & creating new concepts in Physics. He was deeply affected by Lambert's cosine formula, dealing with luminous flux density over a plane surface, in 12th class. He observed that Lambert's formula needed improvement since it was not giving accurate results in each case accordingly. He then decided to modify it in future as he was unable to actually understand & apply the concept of 'Solid Angle'. Although, concept of 'Solid Angle' deeply inspired him for research in 3-D Geometry & then to apply it in Photometry to modify Lambert's formula to give mathematically correct results for 2-D & 3-D figures.       

 

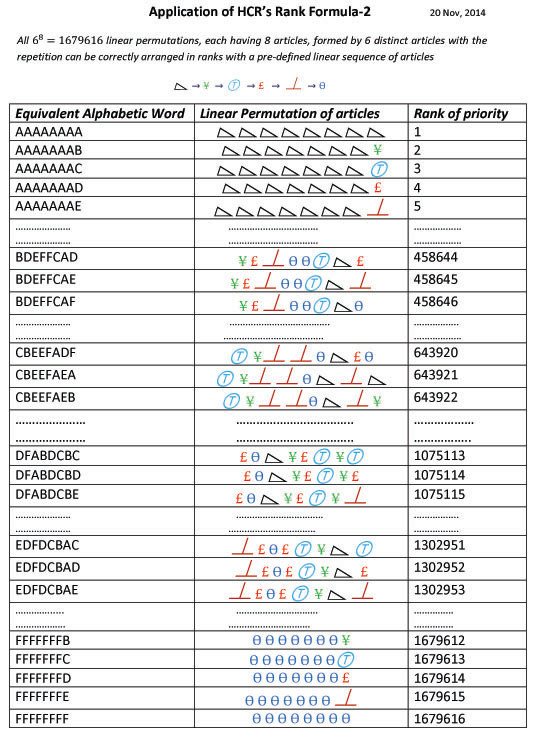
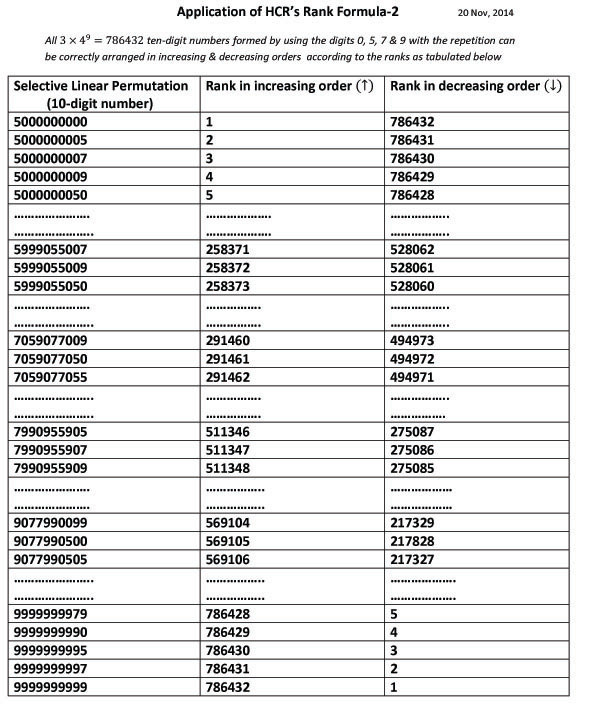
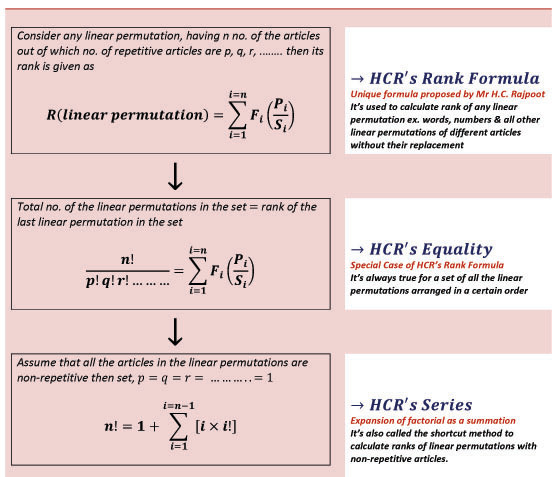
After passing his Intermediate in 2009, he went to Kanpur for preparation of Engineering exams where he, as a result of deep studies, derived a concept of finding out the hierarchical ranks of linear permutations like alphabetic words, numbers & other permutations of non-algebraic articles in 2010. He had to close his research files prior to his engineering exams. As a result, he got admission to Madan Mohan Malaviya Engineering College (at present M.M.M. University of Technology), Gorakhpur-273010 (UP) India in August, 2010.

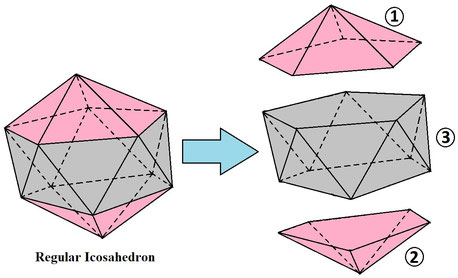
Being inspired by his teachers & elder brother Mr Chandra Shekhar Rajpoot (at present, MBBS), he started to write his first educational book of Geometry. He included all his research articles of Geometry, Trigonometry & Radiometry in this book which was published in March, 2014 by Notion Press, Chennai, India. Then he modified his formula to apply it on all the linear permutations of certain algebraic & non-algebraic articles as well as on the circular permutations under certain conditions. As a result, using his formula, he proved that the factorial of any natural number can be expanded as the sum of finite terms of first natural numbers multiplied by their own factorials. He correlated all the linear permutations of alphabetic letters & digits to that of the various articles having different shape, size, color, surface-design etc. for ease of understanding. He proposed "Theory of Polygon" used to calculate solid angle subtended by any polygonal plane at any point in the space. Using his own theory, he derived the simplest & most versatile formula for all five platonic solids to calculate all the important parameters. This is entitled as "HCR's Formula for Platonic Solids". Although, he didn't have any idea about Euler's formula of platonic solids. Using his theory & formula, he analysed Archimedean solids, Goldberg polyhedra & various truncated & expanded polyhedra. He generalized & tabulated the various important parameters of regular & uniform polyhedra.      

His rank formula, proven as the greatest logical formula which universal for linear as well as circular permutations in the field of Algebra, published in International Journal of Mathematics & Physical Sciences Research, (www.resarchpublish.com  Manuscript ID: 004022014A)   

He, with 19 team members of his class, made ATV (All terrain vehicle) first time at his college M.M.M.E.C. since its establishment in 1962 & participated Auto Competition (at National Level) held @ Indore in 2013. He completed his graduation in Mechanical Engineering with honour in 2014 & he is continuously making his best contributions in the field of mathematics especially in Geometry, Algebra & Radiometry (mathematical analysis). He received his master's degree in Production Engineering from Indian Institute of Technology Delhi.   

He is currently studying for a Ph.D. at Indian Institute of Technology Bombay.

          

Math explain the God's existence, forms and power: HCR1991
Mathematics has relations with God. The mathematics can logically explain the existence, forms, and power of God.

HCR's Mathematical legacy ©Harish Chandra Rajpoot

Advanced Geometry by Harish Chandra Rajpoot (HCR's research book published by Notion Press in March, 2014)
www.notionpress.com
HCR's Rank or Series Formula (Certified by International Journal of Mathematics & Physical Sciences Research in Feb, 2014)
www.researchpublish.com
HCR's Series (Expansion of Factorial of any Natural Number as Summation) Certified by International Organization of Scientific Research in March, 2014
www.iosrjournals.org

Certificate of Publication of Paper entitled 'HCR's THEORY OF POLYGON' published by International Journal of Mathematics & Physical Sciences Research, 12 Oct, 2014 (website: www.researchpublish.com)
Certificate of Publication of Paper entitled 'HCR's THEORY OF POLYGON' published by International Journal of Mathematics & Physical Sciences Research, 12 Oct, 2014 (website: www.researchpublish.com)
Certificate of Publication of Paper entitled 'HCR's Infinite-series' published by International Journal of Mathematics & Physical Sciences Research, 2 Oct, 2014 (website: www.researchpublish.com)
Certificate of Publication of Paper entitled 'HCR's Infinite-series' published by International Journal of Mathematics & Physical Sciences Research, 2 Oct, 2014 (website: www.researchpublish.com)
HCR's Rank Formula-2 used to calculate rank of any linear permutation for repetition of articles
HCR's Rank Formula-2 used to calculate rank of any linear permutation for repetition of articles
HCR's Rank Formula applied on the color property of articles to calculate ranks & arrange them in correct order
HCR's Rank Formula applied on the color property of articles to calculate ranks & arrange them in correct order
HCR's Rank Formula-2 applied on the linear permutations of non-algebraic articles to calculate the ranks & arrange all those in mathematical correct order
HCR's Rank Formula-2 applied on the linear permutations of non-algebraic articles to calculate the ranks & arrange all those in mathematical correct order
Application of HCR's Rank Formula-2 on the numbers with zero & non-zero digits
Application of HCR's Rank Formula-2 on the numbers with zero & non-zero digits
Solid angle covered by a regular pentagonal plane derived by using HCR's Theory of Polygon-2014
Solid angle covered by a regular pentagonal plane derived by using HCR's Theory of Polygon-2014
Solid angle covered by a regular hexagonal plane derived by using HCR's Theory of Polygon-2014
Solid angle covered by a regular hexagonal plane derived by using HCR's Theory of Polygon-2014
Derivation by Mr H. C. Rajpoot for the solid angle subtended by a regular heptagon using HCR's Theory of Polygon
Derivation by Mr H. C. Rajpoot for the solid angle subtended by a regular heptagon using HCR's Theory of Polygon
Derivation by H. C. Rajpoot for solid angle covered by a regular octagonal plane
Derivation by H. C. Rajpoot for solid angle covered by a regular octagonal plane
Verification of HCR's Rank Formula derived by Mr H. C. Rajpoot in Feb, 2010
Verification of HCR's Rank Formula derived by Mr H. C. Rajpoot in Feb, 2010
These are some important estimations made by Mr H. C. Rajpoot
These are some important estimations made by Mr H. C. Rajpoot
HCR's Series (expansion of factorial of any number as a summation ) is derived from HCR's Rank Formula (used to calculate rank of any linear permutation when the replacement of articles is not there in the linear permutations of a set) applying certain co
HCR's Series (expansion of factorial of any number as a summation ) is derived from HCR's Rank Formula (used to calculate rank of any linear permutation when the replacement of articles is not there in the linear permutations of a set) applying certain co
HCR’s Inverse Cosine Formula derived by Mr H.C. Rajpoot is a trigonometric relation of four variables/angles. It is applicable for any three straight lines or planes, either co-planar or non-coplanar, intersecting each other at a single point in the space
HCR’s Inverse Cosine Formula derived by Mr H.C. Rajpoot is a trigonometric relation of four variables/angles. It is applicable for any three straight lines or planes, either co-planar or non-coplanar, intersecting each other at a single point in the space
This formula was derived by Mr H.C. Rajpoot by applying his "Theory of Polygon" to calculate all the important parameters of any regular n-polyhedron such as inner radius, outer radius, mean radius, surface area & volume. This formula is general in form.
This formula was derived by Mr H.C. Rajpoot by applying his "Theory of Polygon" to calculate all the important parameters of any regular n-polyhedron such as inner radius, outer radius, mean radius, surface area & volume. This formula is general in form.
Application of H. Rajpoot's Formula on a regular tetrahedron to calculate all the important parameters i.e. inner radius, outer radius, mean radius, surface area & volume only by measuring its edge length.
Application of H. Rajpoot's Formula on a regular tetrahedron to calculate all the important parameters i.e. inner radius, outer radius, mean radius, surface area & volume only by measuring its edge length.
All the important parameters of a truncated icosahedron such as normal distances & solid angles of the faces, inner radius, outer radius, mean radius, surface area & volume have been calculated by using HCR's formula for regular polyhedrons (all five plat
All the important parameters of a truncated icosahedron such as normal distances & solid angles of the faces, inner radius, outer radius, mean radius, surface area & volume have been calculated by using HCR's formula for regular polyhedrons (all five plat
Table of all the important parameters of a truncated tetrahedron (having 4 congruent equilateral triangular & 4 congruent regular hexagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner radius, o
Table of all the important parameters of a truncated tetrahedron (having 4 congruent equilateral triangular & 4 congruent regular hexagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner radius, o
Table of all the important parameters of a truncated dodecahedron (having 20 congruent equilateral triangular & 12 congruent regular decagonal faces each of equal edge length) such as normal distances & solid angles of the faces, inner & outer radii
Table of all the important parameters of a truncated dodecahedron (having 20 congruent equilateral triangular & 12 congruent regular decagonal faces each of equal edge length) such as normal distances & solid angles of the faces, inner & outer radii
Table of all the important parameters of a truncated dodecahedron (having 20 congruent equilateral triangular & 12 congruent regular decagonal faces each of equal edge length) such as normal distances & solid angles of the faces, inner & outer radii
Table of all the important parameters of a truncated dodecahedron (having 20 congruent equilateral triangular & 12 congruent regular decagonal faces each of equal edge length) such as normal distances & solid angles of the faces, inner & outer radii
HCR's formula for all five platonic solids
HCR's formula for all five platonic solids
Table of all the important parameters of a truncated hexahedron (having 8 congruent equilateral triangular & 6 congruent regular octagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii
Table of all the important parameters of a truncated hexahedron (having 8 congruent equilateral triangular & 6 congruent regular octagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii
Table of all the important parameters of a cuboctahedron (Archimedean solid having 8 congruent equilateral triangular & 6 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii
Table of all the important parameters of a cuboctahedron (Archimedean solid having 8 congruent equilateral triangular & 6 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii
All the important parameters of an icosidodecahedron (having 20 congruent equilateral triangular & 12 congruent regular pentagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii
All the important parameters of an icosidodecahedron (having 20 congruent equilateral triangular & 12 congruent regular pentagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces, inner & outer radii
such as normal distances & solid angles subtended by the faces, inner radius, outer radius, mean radius, surface area & volume calculated by using HCR's formula for regular polyhedrons. It can be used in analysis, designing & modelling of polyhedrons.
Table of all the important parameters of the rhombicosidodecahedron (an Archimedean solid having 20 congruent equilateral triangular, 30 congruent square & 12 congruent regular pentagonal faces each of equal edge length)
Table of all the important parameters of a truncated icosidodecahedron (having 20 congruent equilateral triangular faces, 30 congruent golden rectangular faces & 12 congruent regular pentagonal faces) such as normal distances & solid angles by the faces
Table of all the important parameters of a truncated icosidodecahedron (having 20 congruent equilateral triangular faces, 30 congruent golden rectangular faces & 12 congruent regular pentagonal faces) such as normal distances & solid angles by the faces
Table of all the important parameters of the great rhombicosidodecahedron (the largest Archimedean solid having 30 congruent square, 20 congruent regular hexagonal & 12 congruent regular decagonal faces each of equal edge length)
Table of all the important parameters of the great rhombicosidodecahedron (the largest Archimedean solid having 30 congruent square, 20 congruent regular hexagonal & 12 congruent regular decagonal faces each of equal edge length)
Table of all the important parameters of a small rhombicuboctahedron (an Archimedean solid having 8 congruent equilateral triangular & 18 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces,
Table of all the important parameters of a small rhombicuboctahedron (an Archimedean solid having 8 congruent equilateral triangular & 18 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces,
Table of the important parameters of Great Rhombicuboctahedron (an Archimedean solid having 12 congruent square, 8 congruent regular hexagonal & 6 regular octagonal faces each of equal edge length) such as normal distances & solid angles by the faces.
Table of the important parameters of Great Rhombicuboctahedron (an Archimedean solid having 12 congruent square, 8 congruent regular hexagonal & 6 regular octagonal faces each of equal edge length) such as normal distances & solid angles by the faces.
Table of the important parameters of a truncated cuboctahedron (having 8 congruent equilateral triangular, 6 congruent square & 12 congruent golden rectangular faces) such as normal distances & solid angles subtended by the faces.
Table of the important parameters of a truncated cuboctahedron (having 8 congruent equilateral triangular, 6 congruent square & 12 congruent golden rectangular faces) such as normal distances & solid angles subtended by the faces.
All the important parameters of a snub cube (an Archimedean solid having 32 congruent equilateral triangular & 6 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces.
All the important parameters of a snub cube (an Archimedean solid having 32 congruent equilateral triangular & 6 congruent square faces each of equal edge length) such as normal distances & solid angles subtended by the faces.
All the important parameters of a snub dodecahedron (an Archimedean solid having 80 congruent equilateral triangular & 12 congruent regular pentagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces.
All the important parameters of a snub dodecahedron (an Archimedean solid having 80 congruent equilateral triangular & 12 congruent regular pentagonal faces each of equal edge length) such as normal distances & solid angles subtended by the faces.
Table of all the important parameters of any regular spherical polygon such as solid angle subtended at the center, area, length of side, interior angle etc. derived by Mr H.C. Rajpoot by using simple geometry & trigonometry.
Table of all the important parameters of any regular spherical polygon such as solid angle subtended at the center, area, length of side, interior angle etc. derived by Mr H.C. Rajpoot by using simple geometry & trigonometry.
Table of all the important parameters of a decahedron having 10 congruent faces each as a right kite to calculate normal distance of each face from the center, inscribed radius, circumscribed radius, mean radius, surface area & volume.
Table of all the important parameters of a decahedron having 10 congruent faces each as a right kite to calculate normal distance of each face from the center, inscribed radius, circumscribed radius, mean radius, surface area & volume.
Table of the important parameters of a uniform tetradecahedron, having 2 congruent regular hexagonal faces, 12 congruent trapezoidal faces & 18 vertices lying on a spherical surface with certain radius, derived by the author by applying "HCR's Theory.
Table of the important parameters of a uniform tetradecahedron, having 2 congruent regular hexagonal faces, 12 congruent trapezoidal faces & 18 vertices lying on a spherical surface with certain radius, derived by the author by applying "HCR's Theory.
Table of the formula generalized by the author which are applicable to calculate the important parameters, of any uniform polyhedron having 2 congruent regular n-gonal faces, 2n congruent trapezoidal faces, 5n edges & 3n vertices lying on a sphere
Table of the formula generalized by the author which are applicable to calculate the important parameters, of any uniform polyhedron having 2 congruent regular n-gonal faces, 2n congruent trapezoidal faces, 5n edges & 3n vertices lying on a sphere
Generalized formula to calculate area covered by any spherical rectangle having length l & width b each as a great circle arc on a sphere with a radius R" derived by Mr H.C. Rajpoot applying his "Theory of Polygon" for solid angle.
Generalized formula to calculate area covered by any spherical rectangle having length l & width b each as a great circle arc on a sphere with a radius R" derived by Mr H.C. Rajpoot applying his "Theory of Polygon" for solid angle.
The solid angles subtended at the vertices by all five platonic solids (regular polyhedrons) have been calculated by the author Mr H.C. Rajpoot by using standard formula of solid angle. These are the standard values of solid angles for all platonic solids
The solid angles subtended at the vertices by all five platonic solids (regular polyhedrons) have been calculated by the author Mr H.C. Rajpoot by using standard formula of solid angle. These are the standard values of solid angles for all platonic solids
Table of the generalized formula applicable on any uniform polyhedron having 2n congruent right kite faces, 4n edges & 2n+2 vertices lying on a spherical surface with a certain radius. These formula have been derived by the author Mr H.C. Rajpoot.
Table of the generalized formula applicable on any uniform polyhedron having 2n congruent right kite faces, 4n edges & 2n+2 vertices lying on a spherical surface with a certain radius. These formula have been derived by the author Mr H.C. Rajpoot.
Table for the important parameters for the identical circles touching one another on a whole (entire) spherical surface having certain radius such as flat radius & arc radius of each circle, total surface area & its percentage covered by all the circles.
Table for the important parameters for the identical circles touching one another on a whole (entire) spherical surface having certain radius such as flat radius & arc radius of each circle, total surface area & its percentage covered by all the circles.
Table of the generalized formula derived here by the author are applicable to locate any sphere, with a certain radius, resting in a vertex (corner) at which n no. of edges meet together at angle α between any two consecutive of them.
Table of the generalized formula derived here by the author are applicable to locate any sphere, with a certain radius, resting in a vertex (corner) at which n no. of edges meet together at angle α between any two consecutive of them.
Table for the formula generalized by the author to determine the important parameters for snugly packing the spheres in the vertices of all five platonic solids such as the radius of Nth sphere, total volume packed by all the spheres, packing ratio etc.
Table for the formula generalized by the author to determine the important parameters for snugly packing the spheres in the vertices of all five platonic solids such as the radius of Nth sphere, total volume packed by all the spheres, packing ratio etc.
Spherical Geometry by H.C. Rajpoot
HCR's Formula for Regular Spherical Polygon
This inequality had been derived from a general formula which always holds true for any three real positive numbers.
HCR's Inequality for three positive real numbers
This formula is used to mathematically derive the analytic formula to compute distance between any two points on the sphere or globe given latitudes & longitudes. It is an important formula in Global Positioning System (GPS) to precisely compute distances
HCR's cosine formula to calculate the angle between the chords of any two great circle arcs meeting each other at a common end point at some angle
These are the most generalized formula to compute the volume & surface area of a right circular cone cut by a plane parallel to its symmetrical axis at a certain distance
Volume & surface area of a right circular cone cut by a plane parallel to its symmetrical axis (A cut cone with hyperbolic section)
General formula to compute the correct value of the solid angle subtended by any tetrahedron at its vertex when the angles between consecutive lateral edges meeting at that vertex are known
Solid angle subtended by any tetrahedron at its vertex given the angles between consecutive lateral edges meeting at that vertex
A general (analytic & precision) formula to compute the correct value of solid angle subtended by any triangle at the origin which is equally applicable in all the cases given the position vectors of all three vertices in 3D coordinate system.
Solid angle subtended at the origin by any triangle given the position vectors of its vertices
Formula of Disphenoid derived by H C Rajpoot
Formula/Governing Equation of Disphenoid (Isosceles Tetrahderom) derived by HCR
HCR's Theorem derived by H C Rajpoot
HCR's Theorem (Rotation of two co-planar planes, meeting at angle bisector, about their intersecting straight edges )
HCR's Corollary derived by H C Rajpoot
HCR's Corollary (Dihedral angle between two co-planar planes rotated about their intersecting straight edges )
Application of HCR's Theory of Polygon proposed by H C Rajpoot (year-2014)
Derivations of analytic formula for rhombicuboctahedron by applying HCR's Theory of Polygon proposed by H C Rajpoot
Mathematical discovery in 2D Geometry by H C Rajpoot -2021
Mathematically proved that the maximum possible packing fraction of identical circles of a finite radius over an infinite plane is 90.69%. 01 August, 2021.
Derivation of great circle distance formula in 3D Geometry by H C Rajpoot -Aug, 2016
Mathematical derivation of great-circle distance formula using HCR's inverse cosine formula and vectors
Mathematical discovery in 2D Geometry by H C Rajpoot -2021
Mathematical analysis of circum-inscribed (C-I) trapezium
Plane vs Solid Angle by H C Rajpoot -2022
Comparison between Plane Angle and Solid Angle
Polyhedron by H C Rajpoot -2023
Regular pentagonal right antiprism obtained by truncating a regular icosahedron
Polygonal Antiprism by H C Rajpoot -2023
Generalized formula of regular n-gonal right antiprism derived using HCR's Theory of Polygon
Application of HCR's Theory of Polygon
A regular pentagonal right antiprism is generated by truncating a regular icosahedron
Application of HCR's Theory of Polygon
A net of 10 regular triangular and 2 regular pentagonal faces is folded to generate a regular pentagonal right antiprism
Application of HCR's Theorem
A paper model of a pyramidal flat container with regular heptagonal base of desired dimensions & angle, crafted manually by Mr H.C. Rajpoot by applying HCR's Theorem
Application of HCR's Theorem
A paper model of a pyramidal flat container with regular pentagonal base of desired dimensions & angle, crafted manually by Mr H.C. Rajpoot by applying HCR's Theorem
Application of HCR's Theorem
A paper model of Polyhedron with two regular pentagonal and ten trapezoidal faces crafted manually by Mr H.C. Rajpoot by applying HCR's Theorem
Application of HCR's Theory of Polygon
A paper model of rhombic dodecahedron with 12 congruent rhombic faces crafted manually by Mr H.C. Rajpoot. He marked all 14 vertices to truncate a rhombic dodecahedron.
Application of HCR's Theory of Polygon
Mr H.C. Rajpoot discovered and developed a new polyhedron (right) called 'Truncated Rhombic Dodecahedron (HCR's Polyhedron)' by truncating a rhombic dodecahedron (left)
Application of HCR's Theory of Polygon
A model of Regular Penta-decahedral Solar Dome of 5mm thick acrylic sheet having 15 regular triangular faces each with side 15 cm crafted by H C Rajpoot, 26 Oct, 2021.
H C Rajpoot @ IIT Delhi
3-D Model on Creo 5.0
H C Rajpoot @ IIT Bombay
Laser engraving on sodalime glass
Mr H. C. Rajpoot (DOB: 20 Jan, 1991), 12th Standard (Intermediate) @ Oxford Model Inter College, Syam Nagar, Kanpur (UP), India (March, 2009)
Mr H. C. Rajpoot (DOB: 20 Jan, 1991), 12th Standard (Intermediate) @ Oxford Model Inter College, Syam Nagar, Kanpur (UP), India (March, 2009)
Mr H. C. Rajpoot (Doctor of Philosophy @ IIT Bombay)
Mr H. C. Rajpoot (Doctor of Philosophy @ IIT Bombay)
Certificate of Best paper Award in Young Scholars' National Research Writing Competition 2021.
Certificate of Best paper Award in Young Scholars' National Research Writing Competition 2021.
Certificate of Excellence in Peer-Reviewing for contributing to the book chapter 'Time in Mathematical Models'
Certificate of Excellence in Peer-Reviewing for contributing to the book chapter 'Time in Mathematical Models'

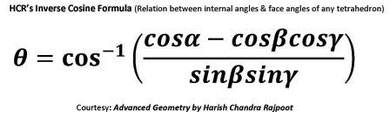
This site has been created, in good faith, merely for keeping the records of biography, mathematical formulae & outstanding achievements of H.C. Rajpoot in the field of Mathematics specifically Algebra, Geometry, Trigonometry & Radiometry in Mathematical Physics.  

 

                                                                                             Copyright ©2014 - 2024. All Rights Reserved        

 

About | Privacy Policy | Sitemap
Log in Log out | Edit
Jimdo

You can do it, too! Sign up for free now at https://www.jimdo.com