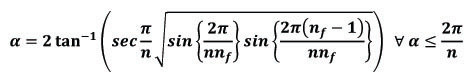HCR's Logo 2019
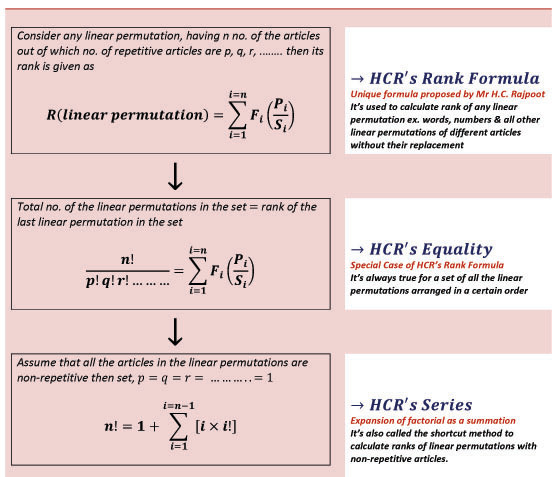
HCR Rank or Series Formula-1
This formula had been derived by the Author in 2010 which he modified in Jan, 2014 @ M.M.M. University of Technology, GKP-273010. This formula is used to find out the rank of any linear permutation like words, numbers with repetitive & non-repetitive letters or digits & all other objects in the world. This is the unique formula applicable for any linear permutation to find out the correct rank or position of any randomly selected linear permutation from a set/group/series of all the linear permutations.
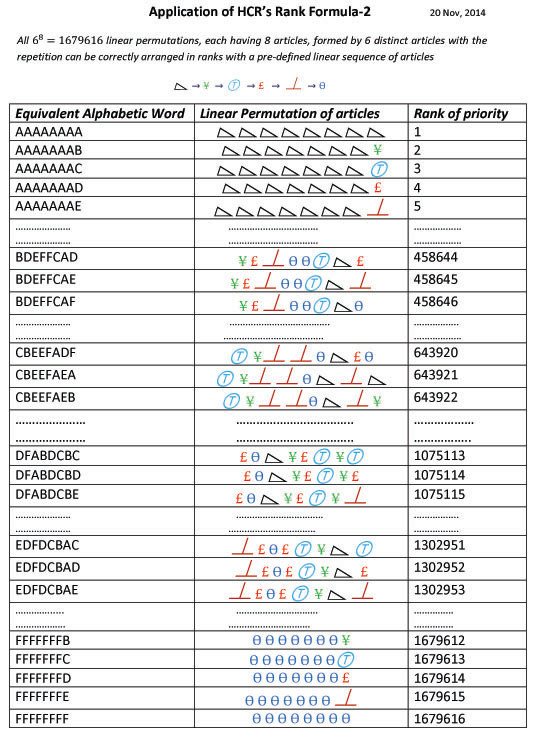
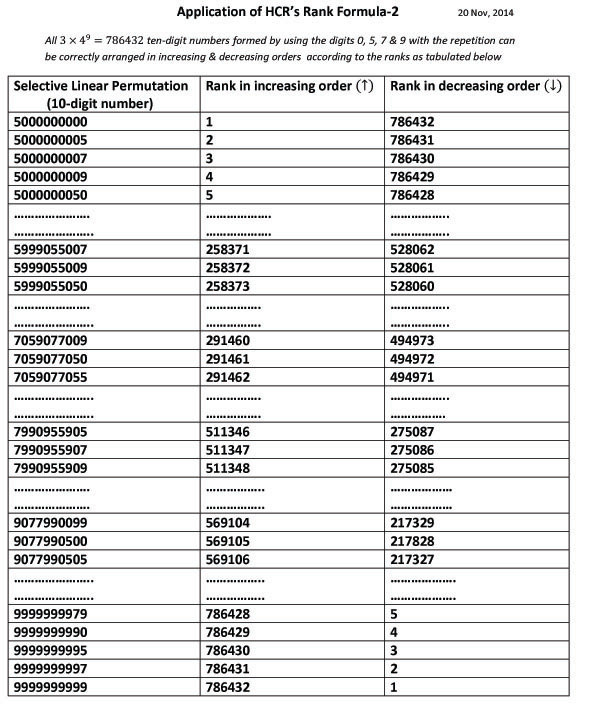
HCR Rank or Series Formula-2
This formula had been derived by the Author in Nov, 2014 . This formula is used to find out the rank of any linear permutation like words, numbers with repetitive & non-repetitive letters or digits & all other objects in the world. This is the unique formula applicable for any linear permutation to find out the correct rank or position of any randomly selected linear permutation from a set/group/series of all the linear permutations when the replacement of articles is allowed unlike HCR's Formula-1
HCR's Series (Expansion of Factorial of any Natural Number)
It shows the expansion of factorial as a summation of finite terms. This is a finite series which is the sum of first ‘n’ natural numbers multiplied by their own respective factorials. The series has been derived from HCR’s Rank formula which was proposed by the author. It is extremely useful in case studies & computations. Although HCR’s Series is different from the Arithmetic, Geometric, Harmonic & Taylor’s Series of simple functions, it is the expansion of factorial of any natural number in form of discrete summation thus it is also named as HCR’s divergence series.
HCR's Infinite-series (Mathematical Analysis of Oblique Frustum of Right Circular Cone)
Three series had been derived by the author, using double-integration in polar co-ordinates, binomial expansion and β & γ-functions for determining the volume, surface-area & perimeter of elliptical-section of oblique frustum of a right circular cone as there had not been any mathematical formula for determining the same due to some limitations. All these three series are in form of discrete summation of infinite terms which converge into finite values hence these were also named as HCR’s convergence series. These are extremely useful in case studies & practical computations.
Application of HCR's Rank Formula to compute rank of circular permutations
Circular to Linear Equivalence shows that a circular permutation is equivalent to a linear permutation when leading element is singleton/non repetitive & the rank of such a circular permutation in which the first or leading element is singleton/non-repetitive is easily calculated by using HCR's Rank Formula applied on any linear permutation. Thus the rank of a circular permutation having repetitive or non-repetitive or both the elements is computed by the rank of equivalent linear permutation. In such cases, HCR's Rank Formula can be easily applied on circular permutations having singleton/non repetitive leading element.
HCR's Theory of Polygon (solid angle subtended by any polygonal plane at any point in the space)
This is the unifying principle proposed by the author to calculate mathematically correct value of solid angle subtended by any polygonal plane at any point in the space. According to this theory, if the location of foot of perpendicular drawn from the given point in the space to the plane of polygon is specified then the polygonal plane can be internally or externally or both divided into certain number of triangles by joining all the vertices of polygon to the foot of perpendicular. Further each of the triangles can be internally or externally sub-divided in two right triangles having common vertex at the foot of perpendicular. Thus, the solid angle subtended by the polygonal plane at any point is the algebraic sum of solid angles subtended by the triangles at the same point such that the algebraic sum of areas of all these triangles is equal to the area of polygon. This theory requires only one standard formula for the solid angle subtended by a right triangular plane.
Spherical Trigonometry by H.C. Rajpoot (Mathematical Analysis of Spherical Triangle)
All the important parameters of a spherical triangle have been derived by Mr H.C. Rajpoot by using simple geometry & trigonometry. All the articles (formula) are very practical & simple to apply in case of a spherical triangle to calculate all its important parameters such as solid angle, covered surface area, interior angles etc. & also useful for calculating all the parameters of the corresponding plane triangle obtained by joining all the vertices of a spherical triangle by straight lines. These formula can also be used to calculate all the parameters of the right pyramid obtained by joining all the vertices of a spherical triangle to the center of sphere such as normal height, angle between the consecutive lateral edges, area of base etc.
Spherical Geometry by H.C. Rajpoot (Mathematical Analysis of Regular Spherical Polygons)
All the parameters of a regular spherical polygon such as solid angle subtended at the center, area, length of side, interior angle etc. have been derived by Mr H.C. Rajpoot by using simple geometry & trigonometry. All the formula are very practical & simple to apply in case of any regular spherical polygon to calculate all its important parameters such as solid angle, surface area covered & length of each side etc. & also all the parameters of the corresponding regular plane polygon obtained by joining all the vertices of the regular spherical polygon by straight lines. These formula can also be used to calculate all the parameters of the right pyramid obtained by joining all the vertices of a regular spherical polygon to the center of sphere such as normal height, angle between the consecutive lateral edges, area of regular polygonal base etc. All these results are also the shortcuts for solving the various complex problems related to the regular spherical polygons.
HCR's formula for regular spherical polygons
It is a very important formula (mathematical relation) applicable on any regular spherical polygon having each of its sides as an arc of the great circle on a spherical surface. It is of crucial importance to find out any of the four important parameters (i.e. radius of sphere, no. of sides, length of side, interior angle of polygon) if other three are given (known) for any regular spherical polygon. It also concludes that any three of the four parameters are self-sufficient to exactly represent a unique regular spherical polygon. A regular spherical polygon having three known parameters can be created or drawn only on a unique spherical surface of a radius which is given by HCR's formula.
Spherical Geometry by H.C. Rajpoot (Mathematical Analysis of Spherical Rectangle)
All the articles have been derived by Mr H.C. Rajpoot by using simple geometry & trigonometry. All the formula are very practical & simple to apply in case of any spherical rectangle to calculate all its important parameters such as solid angle, surface area covered, interior angles etc. & also useful for calculating all the parameters of the corresponding plane rectangle obtained by joining all the vertices of a spherical rectangle by the straight lines. These formula can also be used to calculate all the parameters of the right pyramid obtained by joining all the vertices of a spherical rectangle to the center of the sphere such as normal height, angle between the consecutive lateral edges, area of plane rectangular base etc.
Approximate value of solid angle subtended by a circular plane at any arbitrary point in the space
All the articles (formula) are useful for calculating the approximate value of solid angle subtended by a circular plane at any point in the space. These are also applicable for calculating all the parameters such as major axis, minor axis & eccentricity of elliptical plane of projection of a circular plane when viewed from any off-center position in the space. All the articles have been derived by the author using Approximation Formula of Solid Angle for Symmetrical Planes which had been derived by the author in his book “Advanced Geometry”.
Mathematical Analysis of Elliptical Path in the Annular Region Between Two Circles, Smaller Inside the Bigger One (Ellipse Between Two Circles)
All the articles have been derived by the author by using simple geometry & trigonometry. These articles are related to the analysis of the elliptical path in the annular region between two circle, smaller inside bigger one & their centers separated by a certain distance. These formula are used to calculate minor axis, major axis, eccentricity & the radius of the third tangent circle touching the smaller circle externally & the bigger one internally. These articles (formula) are very practical & simple to apply in case studies & practical applications of 2-D Geometry.
Mathematical Analysis of Three Externally Touching Circles by H.C. Rajpoot
All the articles, related to three externally touching circles, have been derived by using simple geometry & trigonometry to calculate inscribed & circumscribed radii. All the articles (formula) are very practical & simple to apply in case studies & practical applications of three externally touching circles in 2-D Geometry. Although these results are also valid in case of three spheres touching one another externally in 3-D geometry. These formula are also used for calculating any of three radii if rest two are known & the dimensions of the rectangle enclosing thee externally touching circles. Here is also the derivation of a general formula to compute the length of common chord, angle of intersection & area of intersection of two intersecting circles.
Mathematical analysis of decahedron with 10 congruent faces each as a right kite by H.C. Rajpoot
All the important parameters of a decahedron having 10 congruent faces each as a right kite have been derived by the author by applying HCR's Theory of Polygon to calculate normal distance of each face from the center, inscribed radius, circumscribed radius, mean radius, surface area & volume. The formula are very useful in analysis, designing & modeling of polyhedrons.
Mathematical analysis of a uniform tetradecahedron with 2 congruent regular hexagonal faces, 12 congruent trapezoidal faces & 18 vertices lying on a spherical surface by H.C. Rajpoot
All the important parameters of a uniform tetradecahedron, having 2 congruent regular hexagonal faces, 12 congruent trapezoidal faces & 18 vertices lying on a spherical surface with certain radius, have been derived by the author by applying "HCR's Theory of Polygon" to calculate solid angle subtended by each regular hexagonal & trapezoidal face & their normal distances from the center of uniform tetradecahedron, inscribed radius, circumscribed radius, mean radius, surface area & volume. These formula are very useful in analysis, designing & modeling of various uniform polyhedra.
Mathematical analysis of uniform polyhedra with 2 congruent regular n-gonal faces, 2n congruent trapezoidal faces, 5n edges & 3n vertices lying on a spherical surface by H.C. Rajpoot
All the formula are generalized by the author which are applicable to calculate the important parameters, of any uniform polyhedron having 2 congruent regular n-gonal faces, 2n congruent trapezoidal faces each with three equal sides, 5n edges & 3n vertices lying on a spherical surface, such as solid angle subtended by each face at the centre, normal distance of each face from the centre, inner radius, outer radius, mean radius, surface area & volume. These are useful for analysis, designing & modeling of different uniform polyhedra.
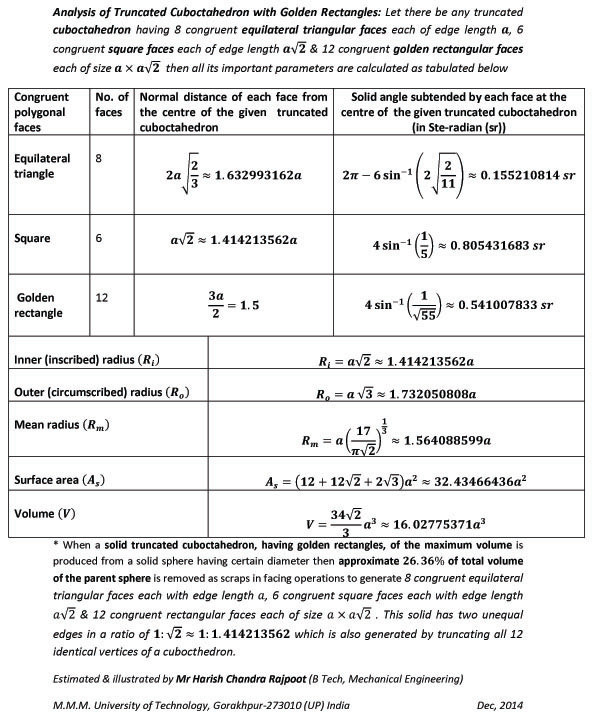
Mathematical analysis of great rhombicuboctahedron with 12 congruent square faces, 8 congruent regular hexagonal faces & 6 congruent regular octagonal faces by H.C. Rajpoot
All the important parameters of a great rhombicuboctahedron (an Archimedean solid), having 12 congruent square faces, 8 regular hexagonal faces, 6 congruent regular octagonal faces each of equal edge length, 72 edges & 48 vertices lying on a spherical surface with certain radius, have been derived by the author Mr H.C. Rajpoot by applying "HCR's Theory of Polygon" to calculate the solid angle subtended by each square face, regular hexagonal face & regular octagonal face & their normal distances from the center of great rhombicuboctahedron, dihedral angles between the adjacent faces, inscribed radius, circumscribed radius, mean radius, surface area & volume. These formula are very useful in analysis, designing & modeling of various uniform polyhedra.
Mathematical analysis of great rhombicosidodecahedron with 30 congruent square faces, 20 congruent regular hexagonal faces & 12 congruent regular decagonal faces by H.C. Rajpoot
All the important parameters of a great rhombicosidodecahedron (the largest Archimedean solid), having 30 congruent square faces, 20 regular hexagonal faces, 12 congruent regular decagonal faces each of equal edge length, 180 edges & 120 vertices lying on a spherical surface with certain radius, have been derived by the author Mr H.C. Rajpoot by applying "HCR's Theory of Polygon" to calculate the solid angle subtended by each square face, regular hexagonal face & regular decagonal face & their normal distances from the center of great rhombicosidodecahedron, dihedral angles between the adjacent faces, inscribed radius, circumscribed radius, mean radius, surface area & volume. These formula are very useful in analysis, designing & modeling of various uniform polyhedra.
Data tables for dihedral angles between the adjacent faces of platonic solids & uniform polyhedra by H.C. Rajpoot
These tables have been prepared by the author Mr H.C. Rajpoot by using his data tables of the various polyhedra for determining the dihedral angle between any two adjacent faces with a common edge of different uniform polyhedra or polyhedral shells. These are very useful for the construction & preparing the wire-frame models of the uniform polyhedral shells having different regular polygonal faces. A polyhedral shell can be easily constructed/framed by continuously fixing all its adjacent (flat) faces each two as a pair at their common edge at an angle equal to the dihedral angle between them. These tables are very useful in analysis, designing & modeling of various uniform polyhedrons.
Mathematical Analysis of Tetrahedron (solid angle subtended by any tetrahedron at its vertex) by H.C. Rajpoot
All the articles have been derived by the author Mr H.C. Rajpoot by using HCR's Inverse cosine formula & HCR's Theory of Polygon. These formula are very practical & simple to apply in case of any tetrahedron to calculate the internal (dihedral) angles between the consecutive lateral faces meeting at any of four vertices & the solid angle subtended by it (tetrahedron) at the vertex when the angles between the consecutive edges meeting at the same vertex are known. These are the generalized formula which can also be applied in case of three faces meeting at the vertex of various regular & uniform polyhedrons to calculate the solid angle subtended by polyhedron at its vertex.
Solid angles subtended by the platonic solids (regular polyhedrons) at their vertices by H.C. Rajpoot
The solid angles subtended at the vertices by all five platonic solids (regular polyhedrons) have been calculated by the author Mr H.C. Rajpoot by using standard formula of solid angle. These are the standard values of solid angles for all five platonic solids i.e. regular tetrahedron, regular hexahedron (cube), regular octahedron, regular dodecahedron & regular icosahedron useful for the analysis of platonic solids.
Solid angles subtended by all 13 Archimedean solids (uniform polyhedrons) at their vertices by H.C. Rajpoot
Table of the solid angles subtended at the vertices by all 13 Archimedean solids (uniform polyhedrons) calculated by the author Mr H.C. Rajpoot by using standard formula of solid angle & formula of tetrahedron. These are the standard values of solid angles which are useful for the analysis of all 13 Archimedean solids truncated tetrahedron, truncated hexahedron (cube), truncated octahedron, truncated dodecahedron, truncated icosahedron, cuboctahedron, icosidodecahedron, small rhombicuboctahedron, small rhombicosidodecahedron, snub cube, snub dodecahedron, great rhombicuboctahedron & great rhombicosidodecahedron.
HCR's Formula for N-Gonal Trapezohedron (Mathematical analysis of trapezohedron having 2n congruent right kite faces, 4n edges & 2n+2 vertices lying on a spherical surface by H.C. Rajpoot
The generalized formula are applicable on any n-gonal trapezohedron having 2n congruent right kite faces, 4n edges & 2n+2 vertices lying on a spherical surface with a certain radius. These formula have been derived by the author Mr H.C. Rajpoot to analyse infinite no. of the trapezohedrons having congruent right kite faces simply by setting n=3,4,5,6,7,………………upto infinity, to calculate all the important parameters such as ratio of unequal edges, outer radius, inner radius, mean radius, surface area, volume, solid angles subtended by the polyhedron at its vertices, dihedral angles between the adjacent right kite faces etc. These formula are very useful for the analysis, modeling & designing of various n-gonal trapezohedrons/deltohedrons.
Reflection of a point about a line & a plane in 2-D & 3-D co-ordinate systems by H.C. Rajpoot
All the articles are related to the reflection of any point about a line in 2-D co-ordinate system and about a line & a plane in 3-D co-ordinate system. Point of reflection about a line or a plane can be easily determined simply by applying the procedures explained or by using formula derived here. These formulas are also useful to determine the foot of perpendicular drawn from a point to a line or a plane in 3-D space. All these articles/derivations are based on the application of simple geometry.
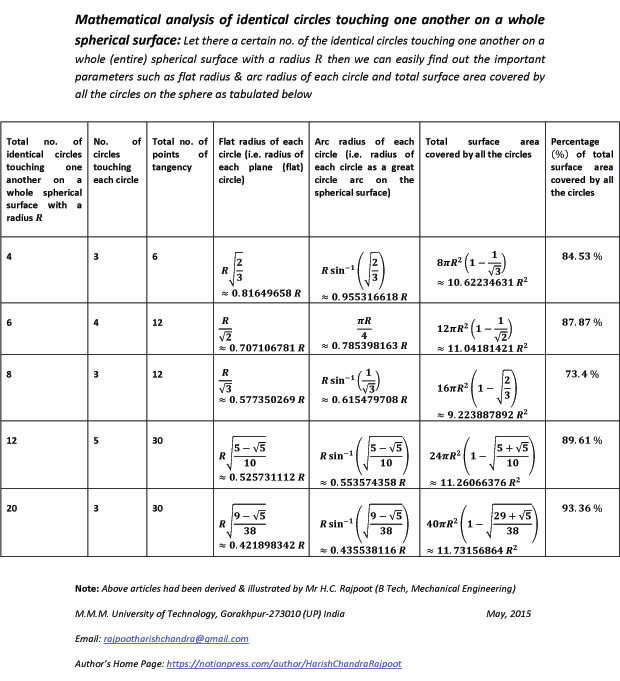
Mathematical analysis of the identical circles touching one another on a whole spherical surface (Spherical Geometry by H.C. Rajpoot)
All the articles discussed & analysed here are related to all five platonic solids. A certain no. of the identical circles are touching one another on a whole (entire) spherical surface having certain radius then all the important parameters such as flat radius & arc radius of each circle, total surface area & its percentage covered by all the circles on the sphere have been easily calculated by using simple geometry & table for the important parameters of all five platonic solids by the author Mr H.C. Rajpoot. These parameters are very useful for drawing the identical circles on a spherical surface & for designing & modeling all five platonic solids having identical flat circular faces.
Mathematical analysis of identical circles touching one another on the spherical polyhedrons analogous to Archimedean solids (Spherical Geometry by H.C. Rajpoot)
The formula, derived here by the author H.C. Rajpoot, are applicable on a certain no. of the identical circles touching one another at different points, centered at the identical vertices of a spherical polyhedron analogous to an Archimedean solid for calculating the different parameters such as flat radius & arc radius of each circle, total surface area covered by all the circles, percentage of surface area covered etc. These formula are very useful for tiling, packing the identical circles in different patterns & analyzing the spherical surfaces analogous to all 13 Archimedean solids. Thus also useful in designing & modelling of tiled spherical surfaces.
Mathematical analysis of sphere resting in the vertex of right pyramid & polyhedron, filleting of the faces & packing of the spheres in the vertex (Advanced Geometry by H.C. Rajpoot)
The formula, derived here by the author H.C. Rajpoot, are applicable on a certain no. of the identical circles touching one another at different points, centered at the identical vertices of a spherical polyhedron analogous to an Archimedean solid for calculating the different parameters such as flat radius & arc radius of each circle, total surface area covered by all the circles, percentage of surface area covered etc. These formula are very useful for tiling, packing the identical circles in different patterns & analyzing the spherical surfaces analogous to all 13 Archimedean solids. Thus also useful in designing & modelling of tiled spherical surfaces.
Derivation of volume of the tetrahedron/pyramid bounded by a given plane & the orthogonal planes in 3-D space (Advanced Geometry by H.C. Rajpoot)
The article here, derived here by the author H.C. Rajpoot, deals with the derivation of a general expression to calculate the volume of tetrahedron/pyramid bounded by a given plane & all three orthogonal planes (i.e. XY-plane, YZ-plane & ZX-plane) using intercept form of equation of a plane in 3-D space. All the derivations are based on simple geometry. These are very useful to directly calculate the volume of the bounded tetrahedron/pyramid.
Mathematical analysis of solid angle subtended by a beam with rectangular profile given the horizontal & vertical beam angles (Radiometry & Photometry by H.C. Rajpoot)
All the articles discussed & analysed here are useful for calculating the important parameters such as solid angle subtended by the beam at the point-source, total area intercepted by the beam with a spherical surface & cone angle of equivalent beam with circular section. These formula are very useful for replacing the rectangular profile by circular profile of a beam emitted by a uniform point-source & vice versa without any change in the total radiation energy/luminous flux associated with the original beam (having either rectangular or circular profile). Thus the articles discussed & analysed here are very useful for the analysis of radiation energy & determining the intensity of (uniform) point-source in a given direction in Radiometry & for the analysis of luminous flux & luminous intensity of (uniform) point-source in a certain direction in Photometry. These are also very useful in replacing the rectangular aperture by a circular aperture & vice versa without any change in the to
HCR's Inequality for three positive real numbers
This conditional inequality had been derived from a general formula which always holds true for any three positive real numbers under certain conditions. There are three possible inequalities out of which one is always satisfied by any three positive real numbers.
HCR's cosine formula to calculate the angle between the chords of any two great circle arcs meeting each other at a common end point at some angle (Spherical Geometry by H.C. Rajpoot)
HCR's cosine formula is a dimensionless formula (mathematical relation of four important angles) which is independent of radius of the sphere & holds good for any spherical surface to find out (plane) angle between the chords of any two great arcs meeting (intersecting) each other at a common end point at some angle. This formula co-relates the angles subtended by two great circle arcs at the center of sphere, angles of concurrence of great arcs & the angle between the chords of great arcs. This formula is very useful to derive the analytic formula to calculate the minimum distance or great circle distance between any two points on the sphere or globe for given latitudes & longitudes. It can also be used to measure the length of any of two great circle arc if the length of other arcs is known.
Application of HCR's inverse cosine formula to compute the minimum distance or great circle distance between any two arbitrary points on the sphere or globe for given values of latitude & longitude
Here is the derivation of great-circle distance formula by using HCR's inverse cosine formula to mathematically derive a symmetrical & analytic formula to compute the minimum distance or great circle distance between any two arbitrary points on a sphere of finite radius which is equally applicable in the geometry of sphere. This formula is useful to calculate the geographical distance between any two points on the globe for the given latitudes & longitudes. This formula gives the correct values for all the distances on the tiny spheres as well as the large spheres like giant planets assuming them perfect spheres.
Minimum distance or great circle distance between any two arbitrary points on the sphere or globe for given values of latitude & longitude using vectors
Here is a derivation of the analytic formula to compute the minimum distance or great circle distance between any two arbitrary points on a sphere of finite radius which is equally applicable in the geometry of sphere. It is a precision formula which gives the correct values for all the distances on the tiny spheres and the large spheres like giant planets. It is also applicable in Global Positioning System to precisely calculate the minimum distance or great circle distance between any two points on the globe for given latitudes & longitudes.
How to distinguish between surface of a sphere & surface of a torus (Flat Ring Test by H.C. Rajpoot)
This is the simplest test used to distinguish between surface of a sphere & surface of a torus simply by placing a flat circular ring once anywhere on the unknown surface of sphere or torus and then observing the contact of periphery of ring with the surface, without walking or checking the entire surface.
Volume & surface area of right circular cone cut by a plane parallel to its symmetrical axis (Hyperbolic section of right circular cone)
All the articles have been derived by the author by using simple geometry, trigonometry & calculus. All the formula are the most generalized expressions which can be used for computing the volume & surface area of minor & major parts usually each with hyperbolic section obtained by cutting a right circular cone with a plane parallel to its symmetrical (longitudinal) axis.
Solid angle subtended by a tetrahedron at its vertex given angles between lateral edges meeting at that vertex & solid angle subtended by a triangle at the origin (Application of HCR's cosine formula)
The author H C Rajpoot derived a general formula to compute the correct value of the solid angle subtended by any tetrahedron at its vertex when the angles between consecutive lateral edges meeting at that vertex are known because there is no approximation in the formula. This is an analytic & precision formula to compute the correct value of solid angle subtended by a triangle at the origin which is equally applicable in all the cases given the position vectors of all three vertices in 3D coordinate system.
Mathematical analysis of disphenoid (isosceles tetrahedron) (Derivation of volume, surface area, vertical height, in-radius, circum-radius, coordinates of vertices,in-center, circum-center & centroid)
The author H C Rajpoot derived formula to analytically compute all the important parameters of a disphenoid (isosceles tetrahedron with four congruent acute-triangular faces) such as volume, surface area, vertical height, radii of inscribed & circumscribed spheres, solid angle subtended at each vertex, coordinates of vertices, in-centre, circum-centre & centroid of a disphenoid for the optimal configuration in 3D space. The author has also proved the important conclusions related to a disphenoid by his mathematical derivations using 3D coordinate geometry.
Mathematical derivations of some important formula in 2D-Geometry by HCR
Here are some important formula in 2D-Geometry derived by the author Mr H.C. Rajpoot using simple geometry & trigonometry. The formula, derived here, are related to the triangle, square, trapezium & tangent circles. These formula are very useful for case studies in 2D-Geometry to compute the important parameters of 2D-figures.
Computation of area of spherical triangle given that aperture angles subtended by the sides or the arc lengths of sides (3D Geometry by HCR)
Here are the general formula derived by the author Mr H.C. Rajpoot to compute the area of the spherical triangle having each side as a great circle arc on the spherical surface when 1.) aperture angle subtended by each of three sides at the center of sphere are known 2.) arc length of each of three sides is known. These formula are applicable for any spherical triangle to the compute area on the sphere.
Three proofs of Apollonius Theorem (2D Geometry by HCR)
The author Mr H C Rajpoot gives the proofs of Apollonius theorem by three different methods 1. using Trigonometry 2. Pythagoras theorem. This theorem is very useful for triangle, parallelogram, rhombus and rectangle.
Solid angle subtended by a regular n-gonal right pyramid at its apex (Application of HCR's Theory of Polygon)
This paper presents the derivation of formula by the author Mr H. C. Rajpoot to analytically compute the solid angle subtended by a regular n-gonal right pyramid at its apex when either normal height, side length of regular polygonal base & number of sides of base area known or the apex angle (i.e. angle between any two consecutive lateral edges meeting at the apex) & number of sides are known.
Solid angle subtended by a rectangular right pyramid at its apex (Application of HCR's Theory of Polygon)
This paper presents the derivation of formula by the author Mr H. C. Rajpoot to analytically compute the solid angle subtended by a rectangular right pyramid at its apex when the apex angles (i.e. angles between two pairs of consecutive lateral edges meeting at the apex) are known.
HCR's Theorem (Rotation of two co-planar planes, meeting at angle bisector, about their intersecting straight edges)
This paper presents the derivation of formula by the author Mr H. C. Rajpoot to analytically In this theorem, we have to analytically compute the V-cut angle (δ) required for rotating through the same angle (θ) the two co-planar planes, initially meeting at a common edge bisecting the angle (α) between their intersecting straight edges, about their intersecting straight edges until their new straight edges (generated after removing V-shaped planar region) coincide. As a result, we get a point (apex) where three planes intersect one another out of which two are original planes (rotated) & third one is their co-plane (fixed).
This theorem is very important for creating pyramidal flat containers with polygonal (regular or irregular) base, closed right pyramids & polyhedrons having two regular n-gonal & 2n congruent trapezoidal faces.
The author has also presented some paper models of pyramidal flat containers with regular pentagonal, heptagonal and octagonal bases
This theorem is very important for creating pyramidal flat containers with polygonal (regular or irregular) base, closed right pyramids & polyhedrons having two regular n-gonal & 2n congruent trapezoidal faces.
The author has also presented some paper models of pyramidal flat containers with regular pentagonal, heptagonal and octagonal bases
Mathematical Analysis & Modeling of Pyramidal Flat Container, Right Pyramid & Polyhedron (Application of HCR's theoremand Corollary)
In this paper, the author Mr H. C. Rajpoot derives the generalized formula to compute all the important parameters like V-cut angle (using HCR’s Theorem), edge length of open end, dihedral angle (using HCR’s Corollary), surface area and volume of pyramidal flat container with regular polygonal base, right pyramids and polyhedrons (bi-pyramids). We will apply these generalized formula to compute important parameters & make paper models of the pyramidal flat containers with square, regular pentagonal, hexagonal, heptagonal & octagonal bases, right pyramids and polyhedrons (bi-pyramids). The concept of making pyramidal flat containers, right pyramids and polyhedrons (bi-pyramids) is mainly based on the rotation or folding of two co-planar planes about their intersecting straight edges (as discussed in details and formulated in HCR’s Theorem)
Mathematical Analysis of Rhombic Dodecahedron (Application of HCR's Theory of Polygon)
In this paper, the author Mr H C Rajpoot mathematically analyses & derives analytic formula for a rhombic dodecahedron having 12 congruent faces each as a rhombus, 24 edges & 14 vertices out of which 6 identical vertices lie on a spherical surface with a certain radius. ‘HCR’s Theory of Polygon’ is used to derive formula to analytically compute the angles & diagonals of rhombic face, radii of circumscribed sphere, inscribed sphere & midsphere, surface area & volume of rhombic dodecahedron in terms of edge length, solid angles subtended at the vertices and dihedral angle between adjacent faces. This convex polyhedron can be constructed by joining 12 congruent elementary-right pyramids with rhombic base & certain normal height.
Mathematical Analysis of Truncated Rhombic Dodecahedron (HCR's Polyhedron) Applying HCR's Theory of Polygon
The author Mr H. C. Rajpoot has discovered a new polyhedron by truncating a rhombic dodecahedron from all its 24 edges so that newly generated 24 identical vertices exactly lie on a spherical surface which is named as 'Truncated Rhombic dodecahedron'. A truncated rhombic dodecahedron is a non uniform convex polyhedron having 12 congruent rectangular faces, 6 congruent square faces, 8 congruent equilateral triangular faces, 48 edges & 24 identical vertices. The author derives the formula to analytically compute the radius of circumscribed sphere passing through all 24 identical vertices, normal distances of rectangular, square & equilateral triangular faces from the centre of polyhedron, surface area, volume, solid angles subtended by rectangular, square & equilateral triangular faces at the centre of polyhedron by using ‘HCR’s Theory of Polygon’, dihedral angle between each two faces meeting at any of 24 identical vertices, solid angle subtended at any of 24 identical vertices.
Mathematical Analysis of Rhombicuboctahedron (Small Rhombicuboctahedron) Applying HCR's Theory of Polygon
The author has applied ‘HCR’s Theory of Polygon’ to derive the radius of circumscribed sphere passing through all 24 identical vertices of a rhombicuboctahedron with given edge length & subsequently derived various formula to analytically compute the normal distances of equilateral triangular & square faces from the centre of rhombicuboctahedron, radius of mid-sphere, surface area, volume, solid angles subtended by each equilateral triangular face & each square face at the centre by using ‘HCR’s Theory of Polygon’, dihedral angle between each two faces meeting at any of 24 identical vertices, solid angle subtended by rhombicuboctahedron at any of its 24 identical vertices.
Mathematical analysis of 2D packing of circles in square, hexagon, and circle: Analytic Formulation and Simulation
This paper encompasses the mathematical derivations of the analytic and generalized formula and recurrence relations to find out the radii of n umber of circles inscribed or packed in the plane region bounded by circular arcs (including sectors, semi and quarter circles) & the straight lines. The values of radii obtained using analytic formula and recurrence relations have been verified by comparing with those obtained using MATLAB codes. The methods used in this paper for packing circles are deterministic unlike heuristic strategies and optimization techniques. The analytic formulae derived for plane packing of tangent circles can be generalized and used for packing of spheres in 3D space and packing of circles on the spherical surface which is analogous to distribution of non-point charges. The packing density of identical circles, externally tangent to each other, the most densely packed on the regular hexagonal and the infinite planes have been formulated and analysed. This study p
Mathematical Analysis of Circum-inscribed Polygons: Circum-inscribed (C-I) Trapezium
The circumscribed and the inscribed polygons are well known and mathematically well defined in the context of 2D-Geometry. The term ‘Circum-inscribed Polygon’ has been proposed by the author and used as a new definition of the polygon which satisfies the conditions of a circumscribed polygon and an inscribed polygon together. In other words, the circum-inscribed polygon is a polygon which has both the inscribed and circumscribed circles. The newly defined circum-inscribed polygon has each of its sides touching a circle and each of its vertices lying on another circle. The most common examples of circum-inscribed polygon are triangle, regular polygon, trapezium with each of its non-parallel sides equal to the Arithmetic Mean (AM) of its parallel sides (called circum-inscribed trapezium) and right kite. This paper describes the mathematical derivations of the analytic formula to find out the different parameters in terms of AM and GM of known sides such as radii of circumscribed & in
Mathematical analysis of regular pentagonal right antiprism
A regular pentagonal right antiprism is a convex polyhedron which has 10 identical vertices all lying on a sphere, 20 edges, and 12 faces out of which 2 are congruent regular pentagons, and 10 are congruent equilateral triangles such that all the faces have equal side. This paper presents, in details, the mathematical derivations of the analytic formula to determine the different parameters in term of side, such as normal distances of faces, normal height, radius of circumscribed sphere, surface area, volume, dihedral angles between adjacent faces, and solid angle subtended by each face at the centre, using the known results of a regular icosahedron. All the analytic formulae have been derived using simple trigonometry, and 2-D geometry which are difficult to derive using any other methods. A paper model of regular pentagonal right antiprism with edge length of 4 cm has been made by folding the net of faces made from a A4 white sheet paper.
Regular N-gonal Right Antiprism: Application of HCR's Theory of Polygon
A regular n-gonal right antiprism is a semiregular convex polyhedron which has 2n identical vertices all lying on a sphere, 4n edges, and (2n+2) faces out of which 2 are congruent regular n-sided polygons, and 2n are congruent equilateral triangles such that all the faces have equal side. The equilateral triangular faces meet the regular polygonal faces at the common edges and vertices alternatively such that three equilateral triangular faces meet at each of 2n vertices. This paper presents, in details, the mathematical derivations of the generalized and analytic formula which are used to determine the different important parameters in terms of edge length, such as normal distances of faces, normal height, radius of circumscribed sphere, surface area, volume, dihedral angles between adjacent faces, solid angle subtended by each face at the centre, and solid angle subtended by polygonal antiprism at each of its 2n vertices using HCR’s Theory of Polygon. All the generalized formulae h
HCR's Mathematical legacy ©Harish Chandra Rajpoot







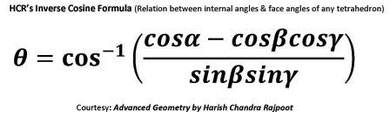




















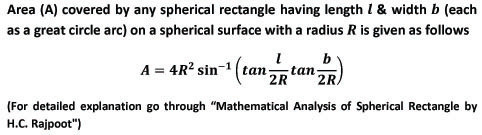




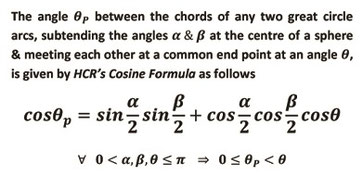
















This site has been created, in good faith, merely for keeping the records of biography, mathematical formulae & outstanding achievements of H.C. Rajpoot in the field of Mathematics specifically Algebra, Geometry, Trigonometry & Radiometry in Mathematical Physics.
Copyright ©2014 - 2024. All Rights Reserved
 Harish Chandra Rajpoot (PhD @ IIT Bombay)
https://iitd.academia.edu/HarishChandraRajpoot
Harish Chandra Rajpoot (PhD @ IIT Bombay)
https://iitd.academia.edu/HarishChandraRajpoot